Récursivité

La récursivité en informatique est un moyen simple et élégant de résoudre de nombreux problèmes qui est conceptuellement très proche de la notion de récursivité en mathématiques. Concrètement on dit qu'une fonction est récursive si elle s'appelle elle même.

Exemple simple

On cherche à calculer la valeur x^n (x à la puissance n) avec n un nombre entier. On peut remarquer que:

1. x^0 = 1
2. x^n = x * x^(n-1) , n>0

On sait calculer la puissance de x pour le cas simple n=0. Pour un cas complexe plus complexe (n>0) on sait se ramener à un cas plus simple. On peut donc calculer la puissance d'un nombre par récursivité:

int puissance(int x, int n)
{
if( n == 0 ) // cas simple
return 1;
else return x*puissance(x, n-1);
}

Exemple plus complexe

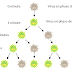
Un hacker écrit un virus informatique dont le seul but est de se multiplier. A chaque fois que le virus arrive sur une machine, il met une minute à l'infecter (phase d'installation) puis il est capable de produire une copie de lui-même toutes les minutes (phase de duplication). La nouvelle copie produite mettra également 1 minute pour infecter un ordinateur puis produira de nouvelles copies toutes les minutes. Combien de virus a-t-on après x minutes ?
Notons f(i) le nombre de virus après i minutes. On observe que f(0)=f(1)=1, f(2)=2, f(3)=3, f(4)=5 mais comment calculer f(i) pour tout i ? A priori, il est difficile de trouver une formule donnant directement le résultat voulu.
En raisonnant par récurrence:

1. Les cas simples : f(0)=f(1)=1
2. Réduction de la complexité. Peut-on exprimer f(t) en fonction de f(t') avec t'<t ? Plaçons-nous au temps t-2, combien y'a-t-il de virus au temps t (valeur de f(t)) ? De manière évidente, f(t) est égal à f(t-1) + les nouveaux virus issus de la duplication des virus ayant fini leur phase d'installation au temps t-1. Comme il faut exactement 1 minute pour finir la phase d'installation, le nombre de virus prêt à se dupliquer au temps t-1 est égal au nombre de virus présent au temps t-2. On obtient donc f(t) = f(t-2) + f(t-1) (c'est la suite de Fibonacci).

On obtient l'algorithme suivant:

int virus(int i)
{
if( n == 0 || n == 1) // cas simple
return 1;
else return virus(n-1)+virus(n-2);
}

Exemple encore plus complexe : les tours de Hanoi

Le problème des tours de Hanoï est un jeu qui consiste à déplacer une pile de disques, tous de diamètres différentes, d'une tour de "départ" vers une tour "d'arrivée" en utilisant une tour "intermédiaire", tout en respectant les règles suivantes:

• on ne peut déplacer qu'un disque à la fois,
• on ne peut pas poser un disque sur un disque plus petit.

Dans la légende (inventée récemment), ce jeu serait pratiqué dans un monastère indien avec 64 disques. La légende dit que la fin du monde arrivera lorsque les moines auront fini le jeu.
A priori, la résolution de ce jeu est un problème compliqué. Néanmoins, on peut faire le raisonnement par récurrence suivant. Posons N=1 le nombre de disques à déplacer.

• Cas simple : si N=1, le problème est trivial, on peut déplacer directement l'unique disque de la tour de "départ" à la tour "d'arrivée".
• Réduction de la complexité: si N>1, alors faisons le raisonnement par récurrence suivant. On suppose que l'on a résolu le problème pour déplacer N-1 disques d'une tour à une autre. Il suffit alors de déplacer les N-1 premiers disques de la tour de "départ" à la tour "intermédiaire", de déplacer le dernier disque de la tour de "départ" vers la tour d'arrivée et finalement de re-déplacer les N-1 disques de la tour "intermédiaire" vers la tour "d'arrivée".

On obtient l'algorithme suivant:

int hanoi(int depart, int intermediaire, int arrivee, int nombreDisques)
{
if( nombreDisques == 1) // cas simple
deplacerDisque(depart, arrivee);
else{
hanoi(depart, arrivee, intermediaire, nombreDisques-1);
deplacerDisque(depart, arrivee);
hanoi(intermediaire, depart, arrivee, nombreDisques-1);
}
}

Exemple d'utilisation pour N=3, on suppose que depart (resp. intermediaire et arrivee) sont des nombres entiers qui représentent les 3 tours:

hanoi(depart,intermediaire,arrivee,3)
hanoi(depart,arrivee,intermediaire,2)
hanoi(depart,intermediaire,arrivee,1)
deplacerDisque(depart,arrivee)
deplacerDisque(depart,intermediaire)
hanoi(arrivee,depart,intermediaire,1)
deplacerDisque(arrivee,intermediaire)
deplacerDisque(depart,arrivee)
hanoi(intermediaire,depart,arrivee,2)
hanoi(intermediaire,arrivee,depart,1)
deplacerDisque(intermediaire,depart)
deplacerDisque(intermediaire,arrivee)
hanoi(depart,intermediaire,arrivee,1)
deplacerDisque(depart,arrivee)